Optimal Two‐Dimensional Optical Orthogonal Codes with the Best Cross‐Correlation Constraint |
| |
| Authors: | Tao Feng Lidong Wang Xiaomiao Wang Yancai Zhao |
| |
| Affiliation: | 1. Department of Mathematics, Beijing Jiaotong University, Beijing, 100044, P. R. China;2. Department of Basic Courses, Chinese People's Armed Police Force Academy, Langfang, P. R. China;3. Department of Mathematics, Ningbo University, Ningbo, P. R. China |
| |
| Abstract: | The study of optical orthogonal codes has been motivated by an application in an optical code‐division multiple access system. From a practical point of view, compared to one‐dimensional optical orthogonal codes, two‐dimensional optical orthogonal codes tend to require smaller code length. On the other hand, in some circumstances only with good cross‐correlation one can deal with both synchronization and user identification. These motivate the study of two‐dimensional optical orthogonal codes with better cross‐correlation than auto‐correlation. This paper focuses on optimal two‐dimensional optical orthogonal codes with the auto‐correlation 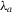 and the best cross‐correlation 1. By examining the structures of w‐cyclic group divisible designs and semi‐cyclic incomplete holey group divisible designs, we present new combinatorial constructions for two‐dimensional and the best cross‐correlation 1. By examining the structures of w‐cyclic group divisible designs and semi‐cyclic incomplete holey group divisible designs, we present new combinatorial constructions for two‐dimensional 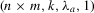 ‐optical orthogonal codes. When ‐optical orthogonal codes. When 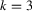 and and 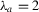 , the exact number of codewords of an optimal two‐dimensional , the exact number of codewords of an optimal two‐dimensional 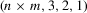 ‐optical orthogonal code is determined for any positive integers n and ‐optical orthogonal code is determined for any positive integers n and 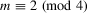 . . |
| |
| Keywords: | optical orthogonal code two‐dimensional optimal incomplete holey group divisible design semi‐cyclic |
|
|

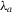 and the best cross‐correlation 1. By examining the structures of w‐cyclic group divisible designs and semi‐cyclic incomplete holey group divisible designs, we present new combinatorial constructions for two‐dimensional
and the best cross‐correlation 1. By examining the structures of w‐cyclic group divisible designs and semi‐cyclic incomplete holey group divisible designs, we present new combinatorial constructions for two‐dimensional 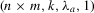 ‐optical orthogonal codes. When
‐optical orthogonal codes. When 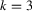 and
and 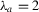 , the exact number of codewords of an optimal two‐dimensional
, the exact number of codewords of an optimal two‐dimensional 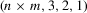 ‐optical orthogonal code is determined for any positive integers n and
‐optical orthogonal code is determined for any positive integers n and 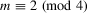 .
.