Dirac reduction for nonholonomic mechanical systems and semidirect products |
| |
| Affiliation: | 1. CNRS and Ecole Normale Supérieure de Paris, Laboratoire de météorologie dynamique, 24 Rue Lhomond, 75005 Paris, France;2. Applied Mechanics and Aerospace Engineering, Waseda University, Okubo, Shinjuku, Tokyo 169-8555, Japan |
| |
| Abstract: | 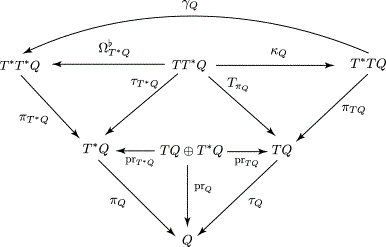
This paper develops the theory of Dirac reduction by symmetry for nonholonomic systems on Lie groups with broken symmetry. The reduction is carried out for the Dirac structures, as well as for the associated Lagrange–Dirac and Hamilton–Dirac dynamical systems. This reduction procedure is accompanied by reduction of the associated variational structures on both Lagrangian and Hamiltonian sides. The reduced dynamical systems obtained are called the implicit Euler–Poincaré–Suslov equations with advected parameters and the implicit Lie–Poisson–Suslov equations with advected parameters. The theory is illustrated with the help of finite and infinite dimensional examples. It is shown that equations of motion for second order Rivlin–Ericksen fluids can be formulated as an infinite dimensional nonholonomic system in the framework of the present paper. |
| |
| Keywords: | Dirac structures Reduction by symmetry Nonholonomic systems Variational structures Semidirect products Rivlin–Ericksen fluids |
| 本文献已被 ScienceDirect 等数据库收录! |
|

